Chapter 2 Using structural equation modeling for path models
2.1 A substantive example of a path model
library(haven)
path.data <- read_dta("path.dta")
# path model
library(lavaan)
path.model <- '
# direct effects
math21 ~ a1 * attention4 + a2 * math7 + a3 * read7
math7 ~ b1 * attention4
read7 ~ c1 * attention4
# indirect effects
ind1 := b1 * a2
ind2 := c1 * a3
'
path.fit <- sem(path.model, estimator = "ML", data = path.data)
summary(path.fit, fit.measures = TRUE, rsquare = TRUE)## lavaan 0.6-9 ended normally after 22 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 8
##
## Used Total
## Number of observations 338 430
##
## Model Test User Model:
##
## Test statistic 23.725
## Degrees of freedom 1
## P-value (Chi-square) 0.000
##
## Model Test Baseline Model:
##
## Test statistic 118.786
## Degrees of freedom 6
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.799
## Tucker-Lewis Index (TLI) -0.209
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -2788.235
## Loglikelihood unrestricted model (H1) -2776.372
##
## Akaike (AIC) 5592.469
## Bayesian (BIC) 5623.053
## Sample-size adjusted Bayesian (BIC) 5597.676
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.259
## 90 Percent confidence interval - lower 0.175
## 90 Percent confidence interval - upper 0.354
## P-value RMSEA <= 0.05 0.000
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.088
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## math21 ~
## attentin4 (a1) 0.081 0.042 1.927 0.054
## math7 (a2) 0.294 0.046 6.399 0.000
## read7 (a3) 0.083 0.016 5.253 0.000
## math7 ~
## attentin4 (b1) 0.113 0.049 2.290 0.022
## read7 ~
## attentin4 (c1) 0.302 0.144 2.098 0.036
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .math21 5.590 0.430 13.000 0.000
## .math7 7.842 0.603 13.000 0.000
## .read7 66.979 5.152 13.000 0.000
##
## R-Square:
## Estimate
## math21 0.191
## math7 0.015
## read7 0.013
##
## Defined Parameters:
## Estimate Std.Err z-value P(>|z|)
## ind1 0.033 0.015 2.156 0.031
## ind2 0.025 0.013 1.949 0.051library(broom)
tidy(path.fit)## # A tibble: 11 × 10
## term op label estimate std.error statistic p.value std.lv std.all
## <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 math21 ~ … ~ "a1" 0.0814 0.0422 1.93 5.40e- 2 0.0814 0.0956
## 2 math21 ~ … ~ "a2" 0.294 0.0459 6.40 1.57e-10 0.294 0.315
## 3 math21 ~ … ~ "a3" 0.0825 0.0157 5.25 1.50e- 7 0.0825 0.259
## 4 math7 ~ a… ~ "b1" 0.113 0.0493 2.29 2.20e- 2 0.113 0.124
## 5 read7 ~ a… ~ "c1" 0.302 0.144 2.10 3.59e- 2 0.302 0.113
## 6 math21 ~~… ~~ "" 5.59 0.430 13 0 5.59 0.809
## 7 math7 ~~ … ~~ "" 7.84 0.603 13.0 0 7.84 0.985
## 8 read7 ~~ … ~~ "" 67.0 5.15 13 0 67.0 0.987
## 9 attention… ~~ "" 9.54 0 NA NA 9.54 1
## 10 ind1 := b… := "ind… 0.0332 0.0154 2.16 3.11e- 2 0.0332 0.0390
## 11 ind2 := c… := "ind… 0.0250 0.0128 1.95 5.13e- 2 0.0250 0.0293
## # … with 1 more variable: std.nox <dbl>library(lavaanPlot)
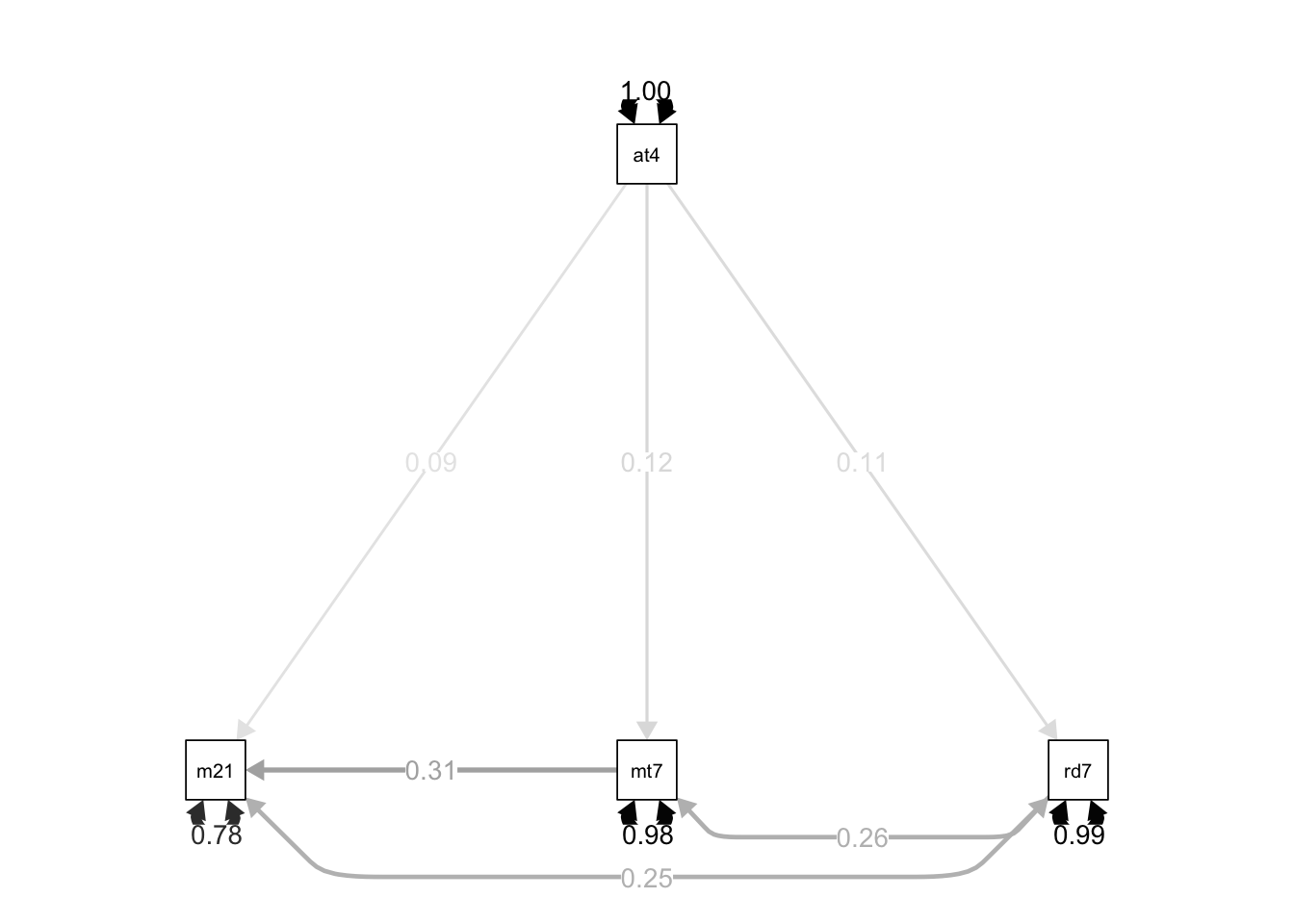
lavaanPlot(model = path.fit, coefs = TRUE, stand = TRUE)library(semPlot)
semPaths(object = path.fit, what = "std", edge.label.cex = 1, curvePivot = TRUE,
fixedStyle = c("black", 1), freeStyle = c("black", 1),
edge.color = "black")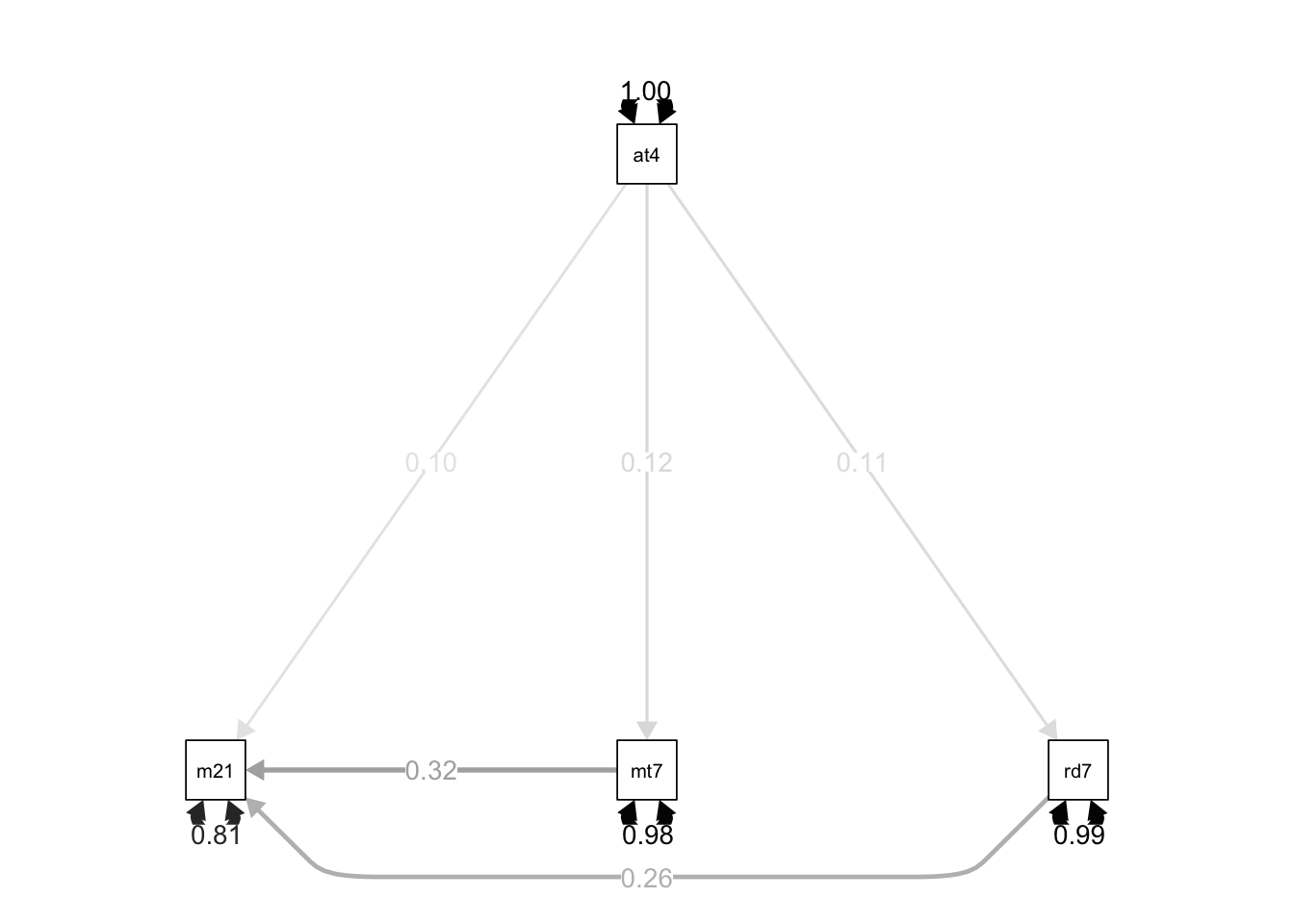
- with SEM a significant chi-squared means that we fail to account for the covariances among our variables
2.3 Auxiliary Variables
- an auxiliary variable is a variable that explains who is more likely to have missing values
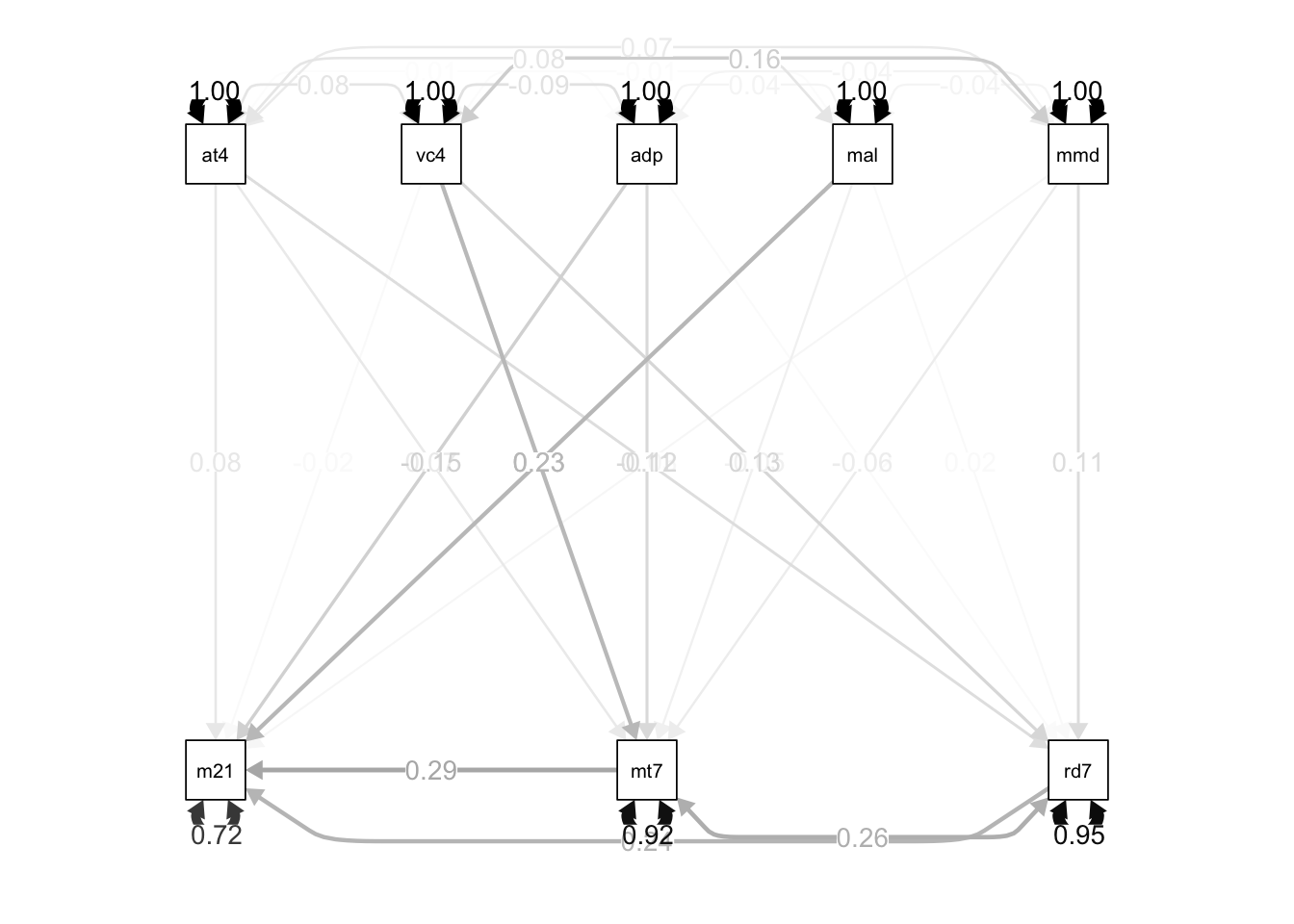
path.model <- '
# direct effects
math21 ~ a1 * attention4 + a2 * math7 + a3 * read7 + vocab4 + adopted + male
+ momed
math7 ~ b1 * attention4 + vocab4 + adopted + male + momed
read7 ~ c1 * attention4 + vocab4 + adopted + male + momed
# indirect effects
ind1 := b1 * a2
ind2 := c1 * a3
# total effects
total_att := a1 + a2 * b1
# residual correlations
math7 ~~ read7
'
library(semTools)## ## ################################################################################# This is semTools 0.5-5## All users of R (or SEM) are invited to submit functions or ideas for functions.## #################################################################################
## Attaching package: 'semTools'## The following objects are masked from 'package:psych':
##
## reliability, skew## The following object is masked from 'package:readr':
##
## clipboard# path.fit <- sem.auxiliary(path.model, aux = "VAR HERE", data = path.data)2.5 A cross-lagged panel design
suppose we want to know the influence of math scores on reading skills and the influence of reading skills on math scores
we can test this with panel data where we have a least two waves of data
path.model <- '
# direct effects
math21 ~ math7 + read7
read21 ~ math7 + read7
# residual correlations
math7 ~~ read7
math21 ~~ read21
'
path.fit <- sem(path.model, data = path.data)
summary(path.fit, fit.measures = TRUE, rsquare = TRUE)## lavaan 0.6-9 ended normally after 40 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 10
##
## Used Total
## Number of observations 336 430
##
## Model Test User Model:
##
## Test statistic 0.000
## Degrees of freedom 0
##
## Model Test Baseline Model:
##
## Test statistic 236.276
## Degrees of freedom 6
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 1.000
## Tucker-Lewis Index (TLI) 1.000
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -3895.659
## Loglikelihood unrestricted model (H1) -3895.659
##
## Akaike (AIC) 7811.319
## Bayesian (BIC) 7849.490
## Sample-size adjusted Bayesian (BIC) 7817.769
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.000
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.000
## P-value RMSEA <= 0.05 NA
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.000
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## math21 ~
## math7 0.305 0.048 6.389 0.000
## read7 0.085 0.016 5.212 0.000
## read21 ~
## math7 0.353 0.142 2.487 0.013
## read7 0.510 0.049 10.495 0.000
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## math7 ~~
## read7 6.295 1.318 4.776 0.000
## .math21 ~~
## .read21 3.090 0.934 3.308 0.001
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .math21 5.668 0.437 12.961 0.000
## .read21 50.046 3.861 12.961 0.000
## math7 7.992 0.617 12.961 0.000
## read7 68.068 5.252 12.961 0.000
##
## R-Square:
## Estimate
## math21 0.216
## read21 0.295tidy(path.fit)## # A tibble: 10 × 9
## term op estimate std.error statistic p.value std.lv std.all std.nox
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 math21 ~… ~ 0.305 0.0477 6.39 1.67e-10 0.305 0.320 0.320
## 2 math21 ~… ~ 0.0852 0.0163 5.21 1.87e- 7 0.0852 0.261 0.261
## 3 read21 ~… ~ 0.353 0.142 2.49 1.29e- 2 0.353 0.118 0.118
## 4 read21 ~… ~ 0.510 0.0486 10.5 0 0.510 0.499 0.499
## 5 math7 ~~… ~~ 6.30 1.32 4.78 1.79e- 6 6.30 0.270 0.270
## 6 math21 ~… ~~ 3.09 0.934 3.31 9.41e- 4 3.09 0.183 0.183
## 7 math21 ~… ~~ 5.67 0.437 13.0 0 5.67 0.784 0.784
## 8 read21 ~… ~~ 50.0 3.86 13.0 0 50.0 0.705 0.705
## 9 math7 ~~… ~~ 7.99 0.617 13.0 0 7.99 1 1
## 10 read7 ~~… ~~ 68.1 5.25 13.0 0 68.1 1 1semPaths(object = path.fit, what = "std", edge.label.cex = 1, curvePivot = TRUE,
fixedStyle = c("black", 1), freeStyle = c("black", 1),
edge.color = "black")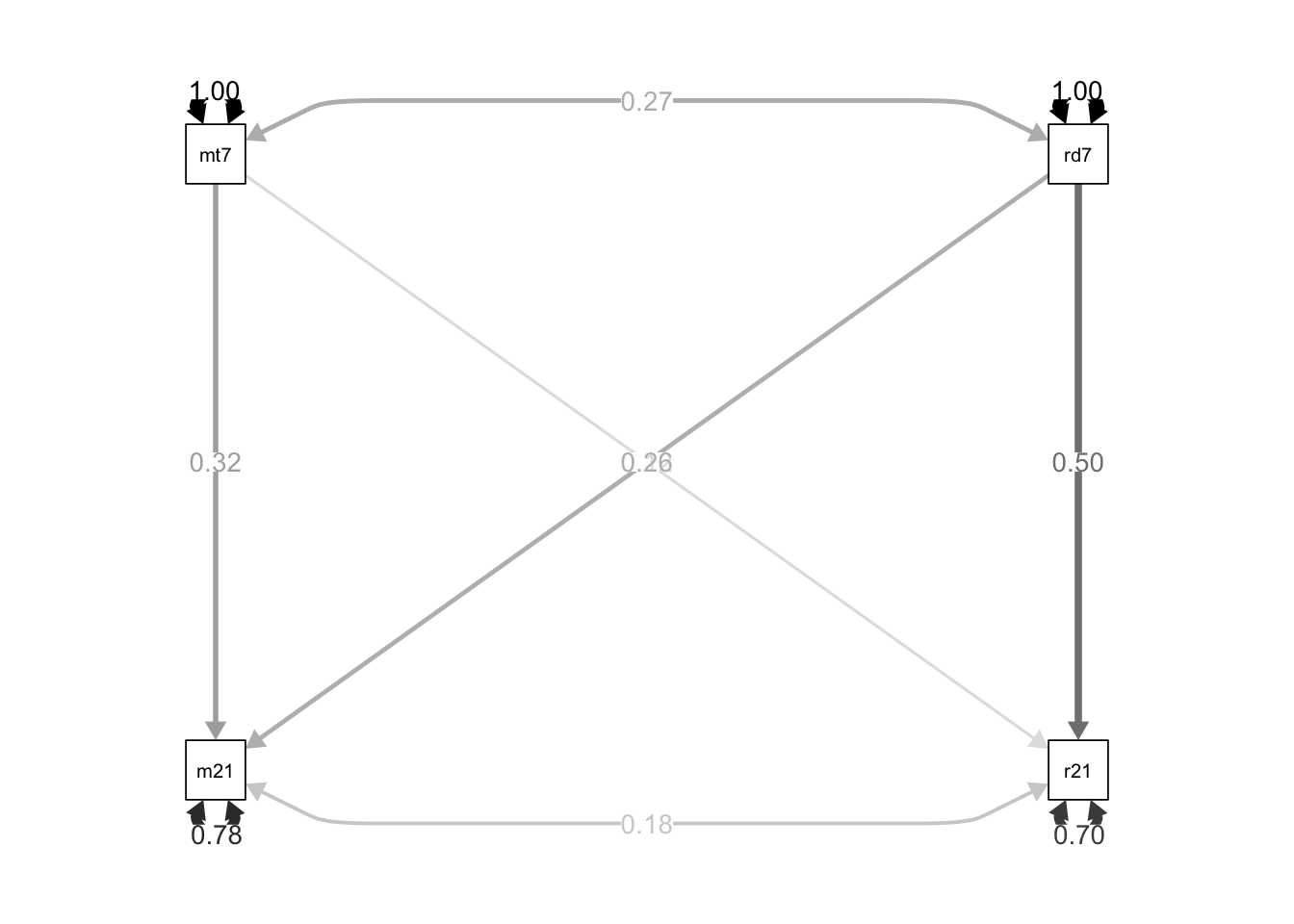
reading skills are more stable than math skills
reading skills are age 7 influence math skills are age 21 more than math skills at age 7 influence reading skills at age 21
2.6 Moderation
auto.data <- read_dta("auto.dta")
library(tidyverse)
auto.data <-
auto.data %>%
mutate(wgt1000s = weight / 1000)
path.model <- '
mpg ~ wgt1000s
'
path.fit <- sem(path.model, data = auto.data)
tidy(path.fit)## # A tibble: 3 × 9
## term op estimate std.error statistic p.value std.lv std.all std.nox
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 mpg ~ wgt1… ~ -6.01 0.511 -11.8 0 -6.01 -0.807 -1.05
## 2 mpg ~~ mpg ~~ 11.5 1.89 6.08 1.18e-9 11.5 0.348 0.348
## 3 wgt1000s ~… ~~ 0.596 0 NA NA 0.596 1 0.596# add predictors
path.model <- '
mpg ~ wgt1000s + foreign
'
path.fit <- sem(path.model, data = auto.data)
tidy(path.fit)## # A tibble: 6 × 9
## term op estimate std.error statistic p.value std.lv std.all std.nox
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 mpg ~ wgt1… ~ -6.59 0.624 -10.6 0 -6.59 -0.885 -1.15
## 2 mpg ~ fore… ~ -1.65 1.05 -1.57 1.17e-1 -1.65 -0.131 -0.287
## 3 mpg ~~ mpg ~~ 11.1 1.83 6.08 1.18e-9 11.1 0.337 0.337
## 4 wgt1000s ~… ~~ 0.596 0 NA NA 0.596 1 0.596
## 5 wgt1000s ~… ~~ -0.209 0 NA NA -0.209 -0.593 -0.209
## 6 foreign ~~… ~~ 0.209 0 NA NA 0.209 1 0.209# now with an interaction
auto.data <-
auto.data %>%
mutate(int = wgt1000s * foreign)
path.model <- '
mpg ~ wgt1000s + foreign + int
'
path.fit <- sem(path.model, data = auto.data)
tidy(path.fit)## # A tibble: 10 × 9
## term op estimate std.error statistic p.value std.lv std.all std.nox
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 mpg ~ wgt… ~ -5.98 0.644 -9.28 0 -5.98 -0.803 -1.04
## 2 mpg ~ for… ~ 9.27 4.38 2.12 3.42e-2 9.27 0.737 1.61
## 3 mpg ~ int ~ -4.45 1.74 -2.56 1.03e-2 -4.45 -0.839 -0.775
## 4 mpg ~~ mpg ~~ 10.2 1.68 6.08 1.18e-9 10.2 0.310 0.310
## 5 wgt1000s … ~~ 0.596 0 NA NA 0.596 1 0.596
## 6 wgt1000s … ~~ -0.209 0 NA NA -0.209 -0.593 -0.209
## 7 wgt1000s … ~~ -0.431 0 NA NA -0.431 -0.516 -0.431
## 8 foreign ~… ~~ 0.209 0 NA NA 0.209 1 0.209
## 9 foreign ~… ~~ 0.484 0 NA NA 0.484 0.977 0.484
## 10 int ~~ int ~~ 1.17 0 NA NA 1.17 1 1.17semPaths(object = path.fit, what = "std", edge.label.cex = 1, curvePivot = TRUE,
fixedStyle = c("black", 1), freeStyle = c("black", 1),
edge.color = "black")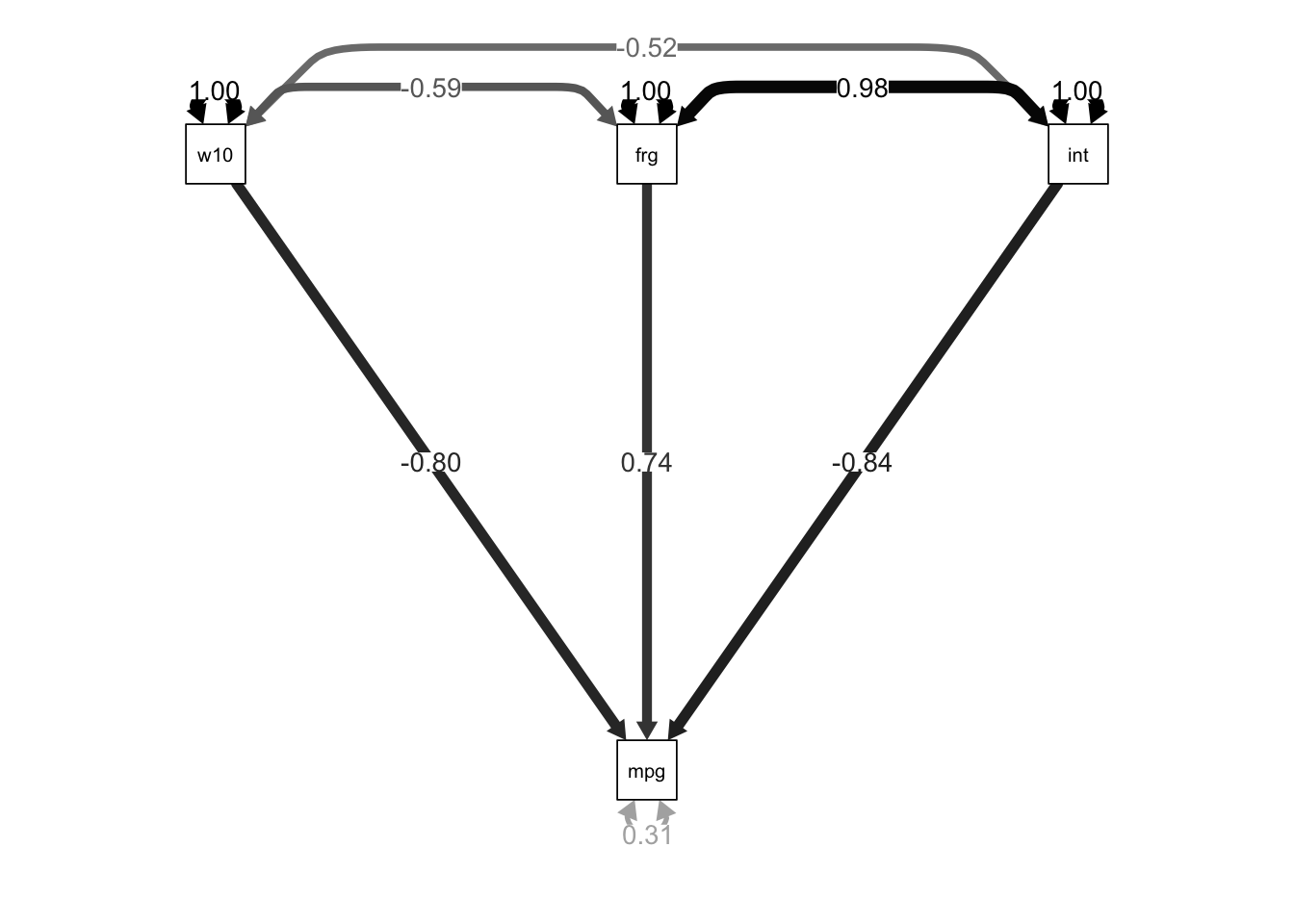
fitted(path.fit)## $cov
## mpg wg1000 foregn int
## mpg 33.020
## wgt1000s -3.580 0.596
## foreign 1.033 -0.209 0.209
## int 1.838 -0.431 0.484 1.174